ngons: Are they really that evil?

Playing around with polygons and trying to code them, I've seen a variety problems that can occur working with polygonal geometry. More than once I've hit a snag in my program and I scratch my head and think, "How do the big guys handle that?" Then I crack open Maya, build the same topology and see it break there as well. What I've come to find is different modeling applications handle polygons in different ways--some are deficiencies and some are just design choices.

Problem with Tris and Quads
A polygon as most people know requires at least three points. This of course makes a triangle. A triangle is an ideal planar figure as the three points--assuming they all don't lie on the same line--form a plane. No matter where you move the points, they will always form a plane. Interpolating attributes between the points is easy. Triangles are simple to rasterize, ray trace, and are pretty much universal across modeling applications.

In geometry a polygon (pronounced /ˈpɒlɪɡɒn/) is traditionally a plane figure that is bounded by a closed path or circuit, composed of a finite sequence of straight line segments (i.e., by a closed polygonal chain). -http://en.wikipedia.org/wiki/Polygon

Stepping up to four points already begins to create problems with modeling applications. This is because unlike a triangle, not all four points have to lie on the same plane. The modeler can be restrictive to the user requiring all points to lie on the same plane (making it extremely difficult for an artist), or it can make certain assumptions about how to render a non-planar quad. Sometimes this may or may not be what the artist wants. There's not really a set definition of how to manipulate/render a non-planar polygon.

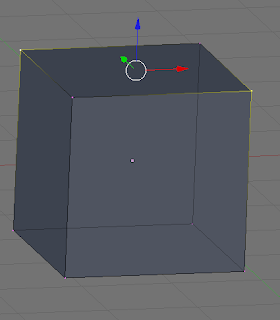
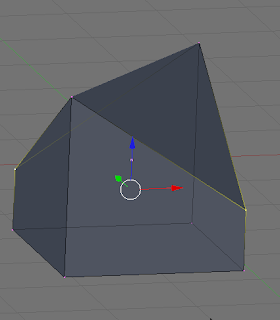
Take a look at the examples below. In the first two images, the user grabs two vertices at opposite ends of the cube and pulls down forming what looks like a roof. For many people, this maybe what they expect as the program--Blender in this case--just treats the quad as two triangles with the long edge going across the two unselected vertices. This may seem perfectly acceptable, but look at the second example. Now we grab the other two vertices and pull down. One might look at the first example and now assume that it will also form the house, but instead it forms some kind of double-steeple with a rain gutter in between.

Pulling down to opposite vertices

Pulling down the other two vertices



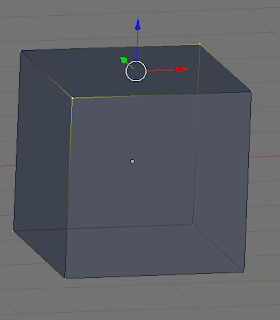
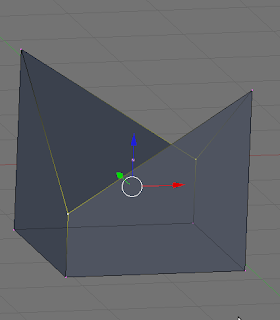
What's going on? Well, Blender just knows it has to render this quad face, so it looks at the first vertex on the face and says, "Okay, let's render these as triangles since rendering non-planar quads doesn't make sense and a planar quad is just two triangles anyway." So it looks at the next two vertices around the face--the one that was pulled down and the opposite unselected vertex and says, "That's three" and renders a nice roof. If you pull the other two vertices down like in the second example, Blender starts rendering at the same vertex as before, but goes up to the unselected vertex, and then back down to the other selected vertex forming that steeple/trench.

Here's the question. Which one is correct? If you pick one and assume that's what the program should always do, you've restricted the artist to never being able to make that other shape easily. You may think Blender's not very smart not knowing how to render non-planar polygons, but that wouldn't be fair. There's no rule. If some program makes a certain decision about how to render that, it's just how they want to deal with it. It doesn't make their solution correct, or Blender's solution incorrect.

You may be thinking, "Hrmm, I bet I could write an algorithm that changes around the order of the rendering to guess what the artist wants...". It's been done. If you go into Maya and try doing this example, you can actually get the model to "pop" in between these two examples as Maya tries to figure out by some threshold what you're trying to do. Is Maya right and Blender wrong? Like I said there's no rule for handling non-planar polygons. If you really want to bend a quad into a two triangles with guaranteed results, just make the two triangles before you bend them (as shown below). Now there's no ambiguity at all. The computer doesn't have to make any decisions about bending anything. You're just moving the points on the triangle, and it knows how to do that no questions asked.

Not only do quads introduce problems like these when they're non-planar, but happens when the quad is not convex? In the example below, I have pulled a vertex over to so the resulting polygon is concave. If I grabbed a different vertex, the renderer might have done what you expencted rendering two nice triangles inside the quad. But because I grabbed that vertex, the renderer made a triangle where it shouldn't have and you see visual tearing, where one triangle is sitting on top of another.

Here you might say, "Well, if the Blender programmers made their modeler smarter, they could just look at that quad, see that it's concave, and render it with the correct triangles". That's certainly a valid point, but that takes processor time to figure out. Assuming the polygon is planar, which as I already stated is iffy, the algorithm has to look at the quad and see how to best divide it up without going outside the polygon. Maya does this and it may seem like a great idea, but that's processing power that could be doing other things like rendering larger meshes. Which would you prefer?

No standards across programs
Not only does the designers have to decide and implement these rules, but what happens when the model leaves the program? Bending a quad may give you what you want in the modeler, but there's no guarantee the program where you're sending that quad handles it the exact same way. Take a ray tracer, for instance. I've never seen an ray intersection that handles a generic four-sided polygon. It will usually divide it up into triangles as would a rasterizer. There's no "correct" way to do handle non-planar polygons or concave polygons, so when you decide you want to model that way, you might get bitten later on. Some programs might handle these issues better than others, but they are just making an arbitrary decision.

N-gons are evil
I have shown that just by moving from a triangle to a quad opens up a whole set of problems--one little extra vertex now allows an artist to create non-planar, concave polygons. "Yuck!", I hope you are saying to yourself. What about ngons? ngons are typically what people call polygons with five or more sides. They have all the same problems as quads, except with infinitely more bad situations. For someone whose never used ngons, he/she may ask, "Well, why don't see just stay far away from ngons to avoid the problems?". This is yet another design decision. Here are a somes reasons why ngons should or should not be included in a modeler.

ngons are good

• "clean" topology - when working with a polygons that are going to be planar anyway, ngons don't display a bunch of edges across it, which makes the model look a little cleaner
• nice cuts - some tools create n-sided polygons. Although they may create poor geometry, they can be extremely convenient
• power to the artist - allowing ngons in modelers gives the artist a chance to work more efficiently even though it may screw him/her up later. Plus, once they're ready to export, they can always clean the mesh up afterwards (some artists prefer this workflow)

An image I stole from the Blender forums. The extrude-vertex tool creates two visible ngons I've marked with a red dot. These ngons are very "clean" in the sense that they are planar, convex, and thus will break down to triangles without any funky results

Two images I stole from blender3darchitect.com. The artist has replaced the distracting quads over the arches with a simple concave ngon. It is debatable whether it is more pleasing to the eye--the former to me looks like keystones. The artist will probably have to clean that up somehow (like triangulating it) before exporting the model

ngons are bad

• no standards - there are no guarantees that ngons will import/export as expected. I have read that Cinema 4D, for example, supports ngons, but triangulates ngons on import
• subdivision - working in realtime subdivion is very popular now a days, but how do you subdivide an ngon? Most algorithms require very strict rules for mesh topology like the popular Catmull-Clark subdivision, that requires all quads. People have implemented/published additions to these algorithms to make them more robust, but it's up to the designer to pick which one is best for them
• tool support - ngons require more complex data structures than quads or triangles meaning tools that work with the polygon have to be smarter--some tools just break or don't handle ngons
• processing power - nothing is for free and at some point the program has to decide how to render the ngons to the screen. If it's a concave polygon, the program has to divide it into triangles that are contained in the original polygon. Would the artist rather be spending this processing power on something else?

What's the conclusion?
I can't take sides with how important or useful ngons are. I've heard several times that once an artist models with ngons, it's hard to go without them. I'm not sure if that's a good thing or not. ngons seem to make things easier at certain stages of modeling, while they often need to be cleaned up later in the pipeline. Working with just triangles and quads can be extremely difficult in many situations, but several powerful tools like loop cut and loop select only work because of the special nature of quad loops, which is why some artists try to keep the model as quads as long as possible.

Below is a screenshot from CGSociety, which has a wiki comparing the various modeling programs. It's apparent that nearly every application now supports ngons. zBrush is excused since I'm sure it has insane data structures to handle what only zBrush can handle, and Blender supposedly has ngon support on the way, so regardless of whether an artist needs it or should use it, support for them is/will be pretty much standard.

Table of modeling applications that provide ngon support taken from CGSociety's wiki